Motor Fundamentals

Electric motors are designed to convert electrical energy into mechanical energy to perform some physical task or work. In order to understand the types of motors that are available as well as their performance characteristics, some understanding of the basic physical principles governing motor design and operation are required. Basic electric motor design encompasses the laws of electricity and magnetism.
Motor feedback and control systems involve semiconductor devices, microprocessors and other elements of electronics.
And no discussion of motors would be complete without a brief understanding of the mechanical principles governing linear
and angular motion.

Basic Electricity

Electric Current

Atomic theory describes matter as an aggregate of atoms. Each atom consists of a nucleus containing positively charged
protons and electrically neutral particles called neutrons. Revolving in orbits around the positive nucleus are negatively charged
electrons.

In metallic conductors (such as copper), one or more electrons from the outer orbits become detached from each atom and
move randomly from one atom to another. These are called free electrons. The positive nucleus and the rest of the electrons
remain relatively fixed in position. Insulators, on the other hand, contain virtually no free electrons.

When an electric field is applied to a conductor, free electrons will drift under the influence of that electric field. Drifting
electrons will collide with stationary atoms causing additional free electrons to drift in the same direction. This movement of electric
charge is called current.

The unit of measurement for current or rate of charge flow is the ampere. We speak of a direct current (DC) if the charges
always flow in the same direction, even though the amount of charge flow per unit time may vary. If the flow of charge reverses
its direction periodically, then we have what is called alternating current (AC). A more detailed description of direct and
alternating current is presentedhere.

Conventional Current Flow:
Before the acceptance of the electron theory, it was assumed that the direction of current flow was from a positively charged
body to a negatively charged body. This positive to negative flow of current is called conventional current flow. However, in a
metallic conductor, it is electrons that carry the charge from negative to positive. The flow of current from negative to positive is
called electron flow. We will adopt conventional current flow throughout this Handbook. In the diagrams, the direction
of current will always be from positive to negative.

Potential Difference (V)

Electrons will move between two points of a conductor if there is a potential difference (or a difference of “electric pressure”)
between the two points. Voltage is the measure of the amount of pressure needed to push electrons through a conductor. It is
analogous to a water pump that maintains a pressure difference between its inlet and outlet and results in water flow. Potential
difference and voltage are often used interchangeably.

The unit of potential difference or voltage is the volt. A potential difference of one volt will be dropped across two points
if a constant current of one ampere flowing between the two points results in a power dissipation of one watt.

Resistance (R)

Resistance is defined as the opposition to current flow. Although electrons may flow in any substance, different materials
offer different resistance to their flow.

Those which make the transfer of electrons relatively easy are called conductors (copper, aluminum, steel, etc.), and those
which tend to impose substantial resistance are called insulators (wood, paper, mica, glass, etc.). Materials with a level of conductivity
between these two extremes are called semiconductors (germanium, silicon). These “in between” materials have become increasingly useful in the application of electrical energy.

The unit of electrical resistance is the ohm (Ω). One ohm is defined as the resistance of a conductor which will allow a
current flow of one ampere when a potential difference of one volt is applied. The resistance of a material is normally dependent
on temperature. In general, the resistance of metallic conductors increases with temperature.

Ohm's Law:
Ohm’s law explains the relationship between voltage, current and resistance. It states that the amount of current through a conductor is directly proportional to voltage applied and inversely proportional to the resistance of the conductor or circuit:
I=V/R
A conductor obeys Ohm’s law when, for a given temperature, the current it conducts varies linearly with the applied voltage.

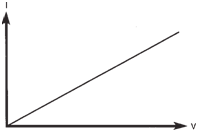Current varies linearly with applied
voltage in accordance with Ohm’s law.

Power:
Electricity is used to perform some type of work or to generate heat. Power is the rate at which work is done or the rate at which heat is generated. The unit for power is the watt. The amount of power dissipated is directly proportional to the amount of current flow and voltage applied:
P=VI

Power Loss:
Power can also be expressed as a function of resistance and current. From Ohm’s law we learned that V = IR. So if you substitute IR for V in the power formula you have:
P=(IR)I or P=I²R
The windings in an electric motor consist of many turns of copper wires. Although copper is an excellent conductor, the substantial total length of wire required in the windings results in measurable power loss because the resistance of a wire increases with its length. This I2R loss in the motor is sometimes referred to as the copper loss.

Horsepower:
Electric motors are rated in horsepower. One horsepower equals approximately 746 watts. Horsepower and watts are simply two different ways to express power.

Series Circuits:
The figure below shows a simple series circuit with a voltage source and resistors R1 and R2. A series circuit is one that allows only one path for current flow. There are three rules which govern series circuits.

The total circuit resistance is the sum of the individual resistance's in the circuit:
R_T = R₁ + R₂ + ... + R_N
Current has the same value at any point within a series circuit.
The sum of the individual voltages across resistors in a series circuit equals the applied voltage:
V = V₁ + V₂

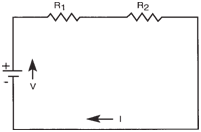Simplified series circuit.

Parallel Circuits:

A simple parallel circuit is one that allows two or more paths for current flow. The resistors shown below are said to be connected in parallel. There are also three rules which govern parallel circuits.

The voltage drop across each branch of a parallel circuit is the same as the applied voltage:
V = V₁ = V₂
The total current in a parallel circuit is equal to the sum of the branch currents:
I = I₁ + I₂
where I₁ and I₂ are currents flowing part of through R₁ and R₂ respectively.
The total resistance in a parallel circuit is always less than or approximately equal to the value of the smallest
resistance in any branch of the circuit.

Since I = _I1 + I₂ you can substitute V/R in place of I and arrive at: V/R_T = V₁/R₁ + V₂/R₂

Since V = V₁ = V₂, you can substitute V(1/R₁ + 1/R₂) in the second part of R₁ R₂ the above equation leaving you with:

V/R_T = V(1/R₁ + 1/R₂) or 1/R_T = 1/R₁ + 1/R₂

Therefore, the reciprocal of the total resistance is the sum of the reciprocal of the individual resistance's. Solving for R results in:

R = 1/(1/R₁ + 1/R₂)

In general, for N resistors in parallel, the equivalent resistance (R) is computed as follows:

1/R = 1/R₁ + 1/R₂ + 1/R₃ + 1/R_N

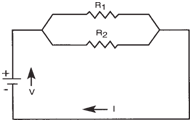Simplified parallel circuit.

Capacitance

A capacitor is a device that stores electric charge. Almost any insulated body can hold a limited electric charge, and the greater the surface area, the greater the charge that can be stored. In practical use, however, a capacitor is a compact system of conductors and insulators (dielectric) so arranged that a large amount of electric charge can be stored in a relatively small volume.

The capacitance (C) is the measure of a capacitor’s ability to store a charge on its plates at a given voltage (V):
C = Q/V

Q, measured in coulombs, is the charge stored in the capacitor. One coulomb has an equivalent charge of about 6.24 x 10¹⁸ electrons.

The unit of capacitance (C) is the farad (F). One farad is the capacitance of a capacitor in which a charge of one coulomb produces a change of one volt in potential difference between its plates.

One farad is an extremely large unit of capacitance. Based on the large physical size needed to produce such a component, smaller units of more convenient size such as the microfarad (μF = 10^-6F), and picofarad (pF = 10^-12F) are used in most applications.

A simple capacitor can be made by placing two identical metal plates in parallel with an air gap between them. See figure below. It is known that the capacitance of a parallel plate capacitor increases proportionally with the area (A) of the plate and decreases proportionally with the distance (d) between them. We may thus write, C = kA / d, where k is a constant.

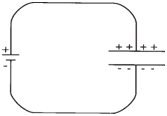Parallel plate capacitor.

It is also known that if a dielectric such as glass is placed between the plates (see figure below), the capacitance is increased five to ten times. In varying degrees, putting materials like mylar, mica, wax or mineral oil between the plates will all result in higher capacitance. Different insulating materials (dielectrics) offer different increases in capacitance. The ratio of the capacitance with the dielectric to that without the dielectric is called the dielectric constant (k) of the material. A vacuum has a dielectric constant: k=1.

Dielectrics used in commercial capacitors include air, oil, paper, wax, shellac, mica, glass, bakelite, polyester and polypropylene film. Most capacitors are fabricated with strips of metal foil, as plates, separated by dielectric strips of the materials mentioned above. The foil and dielectric strips are sandwiched, rolled and encased into a compact form which is then fitted with terminals.

Increased capacitance with
dielectric.

RC Circuit:

The circuit shown above consists only of a battery and a capacitor. Theoretically, with no resistance in the circuit, the capacitor would charge instantly. In reality however, when an electric potential is applied across an uncharged capacitor, the capacitor will not be charged instantaneously, but at a rate that is determined by both the capacitance and the resistance of the circuit.

Similarly, when a capacitor discharges it will not take place instantly. Rather, the discharge current will diminish exponentially over time.

The figure below illustrates a basic RC circuit. The capacitor will be charged if the switch is closed at the “a” position. If the switch is then closed at the “b” position, the capacitor will discharge.

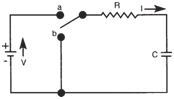Basic RC Circuit

With the resistor present in the circuit, current will not flow as freely. More time will be required to charge the capacitor. Likewise, it will take longer for the capacitor to discharge with the resistor in the circuit.

With a resistor in the circuit, the voltage across the capacitor rises more slowly. The current flow acts directly opposite. When the switch is first thrown to the “a” position there is more current flow. As the voltage across the capacitor reaches the battery potential, current flow decreases. When the capacitor voltage equals the battery voltage level, current flow stops.

Q is the amount of charge on the capacitor and is zero at time t = 0 (see figure below). Q will increase as the current flows until it reaches a maximum value (Q = CV), at which point the current is zero.

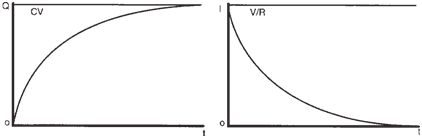Curves for Q and I during charging

In DC circuits, capacitors oppose changes in voltage. The time delay for the capacitor’s voltage to reach the supply voltage is very useful because it can be controlled. It depends on two factors:

the resistance in the circuit, and
the size of the capacitor.

Time Constant:

The time it takes a capacitor to charge to 63% of the supply voltage is called the capacitive time constant (T). It can be calculated using the formula:
T = RC

A capacitor discharges in a similar manner as shown below. The current is now negative, because it flows in the opposite
direction during discharging.

A capacitor is said to be fully charged or fully discharged after five RC time constants.
The figures illustrate that current varies exponentially with time during the charging and discharging of an RC circuit when a DC source is applied.

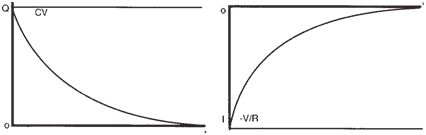Curves for Q and I during discharging