Motor Resources

AC Motors

DC Motors

Special Motors

Motor Fundamentals

GENERATORS AND BASIC AC CIRCUITS

Electric motors are generally divided into DC and AC (induction) types. Each has its own operating characteristics and advantages. In this section, a brief review of direct current vs. alternating current will be presented followed by discussions of various AC circuits.

Direct Current:

Direct current can be obtained through the chemical reactions in primary cells or secondary cells. Primary cells are batteries that consume their active materials when releasing electric energy and hence, are not reusable. Secondary cells (or storage cells), on the other hand, can be recharged by applying electricity in the reverse direction, thus reversing the chemical reaction.

Direct current is commonly produced by DC generators in which mechanical energy supplied by steam turbines, water wheels, water turbines or internal combustion engines is converted into electric energy. A brief description of a simple DC generator will be presented later.

In addition to the above, direct current can be generated from thermal energy (i.e., thermocouple) and light energy (solar cells). Furthermore, alternating current can be converted into direct current through the use of rectifiers.

Alternating Current:

The most commonly supplied form of electric energy is alternating current. The main reason for the widespread use of AC is the fact that the voltage can be readily stepped up or down through the use of transformers. Voltage is stepped up for long distance transmissions and stepped down for sub distribution. The voltage is stepped down even further for industrial and home use. For a given power (VI), stepping up the voltage decreases the current and consequently reduces the (I²R) power loss in the power lines.

There are many additional advantages to AC. For example, AC is used to run induction motors (which do not require a direct supply of current to the rotating member and consequently avoid the problems associated with brush and commutator wear in DC motors).
However, there are cases (battery charging, electroplating, etc.) where DC must be used. Motor applications in which adjustable speed control is important are generally operated from a DC source. However, in most of these cases, the energy is originally generated as AC and then rectified and converted to DC.

Alternating current can be supplied by generators (which will be discussed next) and by devices called inverters which convert
DC into AC.

AC and DC Generators

The figure below shows a simple AC generator. In simple terms, a magnetic field or flux is established between the poles of a magnet. When a coil of conductive material is introduced into the air gap perpendicular to the flux and rotated mechanically at a uniform speed, it will cut the flux and induce an emf that causes a current to flow in the closed circuit formed by the slip rings (X and Y), the brushes and the load resistor (R). With a full 360 degree revolution of the coil, the current flows first in one direction and then in the other, producing an alternating current.

If the coil in the figure below were rotated counterclockwise at a constant speed, the top of the coil (cd) would cut the flux in a downward direction, while the bottom (ab) would cut the flux in an upward direction. By the right-hand rule of induction, the resulting current produced in the coil by reaction with the flux would flow from a to b and from c to d during the first 180 degrees of rotation.

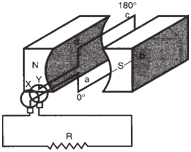Simple alternating current AC generator.

As the coil continued around to its original position, ab would cut the flux downward and cd upward, causing an opposite current flow from d to c and b to a. One 360 degree rotation of the coil is equivalent to one cycle. Since standard available current is 60 Hz (cycles per second), the coil would be rotated sixty full rotations per second to deliver standard 60 Hz AC. This back and forth flow of current can be represented graphically as a sine wave in the figure below.

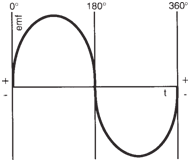Sine wave characteristic of AC current during one cycle (360°).

Without going into the mathematical details, the wave shape of the induced emf can be explained by the fact that the rate of change of flux (Ω) through the surface a-bc- d formed by the wire loop is a sinusoidal function of time. Since by Faraday’s law the induced emf is proportional to the rate of change of flux, a sinusoidal induced emf results.

For DC generators, the same principle of flux cutting holds true, except that instead of the slip rings, a synchronous mechanical switching device called a commutator is used. See figure below.

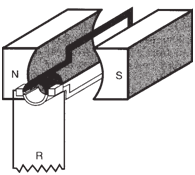Simple DC generator.

The arrangement of commutator and brushes allows the connections to the external circuit (in our case, the resistor, R) to be interchanged at the instant when the emf in the coil reverses, thus maintaining a unidirectional (although pulsating) current (see
figure below).

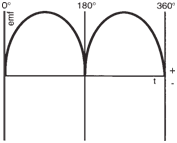Induced emf from the simple DC generator.

The pulsating emf from the simple DC generator is not very useful when relatively uniform DC voltage is required. In practice,
a DC generator has a large number of coils and a commutator with many segments. Each coil is connected to its own
pair of commutator segments. The brushes make contact with each coil for a short period of time when the emf in that coil is
near its maximum value. The figure below illustrates the emf output of a DC generator with four evenly spaced coils connected to
an eight-segment commutator. The dotted curves are the induced emfs (eight emfs for every revolution). The solid line is the output
voltage of the generator.

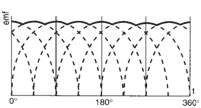Output of DC generator with four coils and an eight-segment commutator.

Two-Phase and Three- Phase AC:

In addition to single-phase AC produced by the generator described above, alternating current may be supplied as both two and three-phase. Using the example of the simple single coil AC generator described before, if we were to add a second coil with its loop arranged perpendicular to the original (see figure below) and rotate them mechanically with a uniform speed, two-phase voltage would be produced.

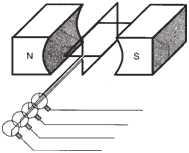Simple two-phase AC generator.

The resulting two-phase voltage sequence is shown below, where one phase lags the other phase by 90 degrees.

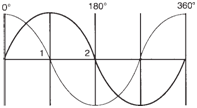Wave shapes produced by two-phase AC.

If we were to add one more coil and space the three at 120 degrees to each other, the same generator
would now produce three-phase current (see figure below).

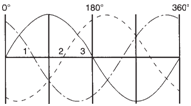Wave shapes produced by three-phase AC.

Two and three-phase current are used in both poly phase and induction motor design. Since both will produce a rotating produce a rotating magnetic field in the stator bore, the rotor will follow the field and result in rotation.

The Delta (Δ)-Connection and Wye-Connection:

Although it is shown above that each coil of the three-phase AC generator is provided with its own pair of slip rings and brushes, the practical design of a three-phase generator has only three slip rings and brushes. This is accomplished by either the Delta-connection or Wye-connection of the three coils (1, 2, and 3) in the generator.

The figure below shows a Delta-connection with output terminals (a, b and c). The three pairs of terminals (a-b, b-c, and c-a) provide a three-phase output like the one shown in Fig. 1-31. The line voltage (voltage from any pair of the terminals) is the same as the coil voltage (voltage across each coil). The line current, however, is 3 times the coil current.

The Wye-connection shown below again has terminals a, b, and c. There is also a common point called the neutral in the middle (O). Again, the terminal pairs (a-b, b-c, and c-a) provide a three-phase supply. In this connection, the line voltage is 3 times the coil voltage while the line current is the same as the coil current. The neutral point may be grounded. It can be brought out to the power user via a four-wire power system for a dual voltage supply.

For example, in a 120/208-volt system, a power user can obtain 208 volt, threephase output by using the three wires from a, b, and c. Furthermore, single-phase, 120 volt power can be tapped from either O-a, O-b or O-c.

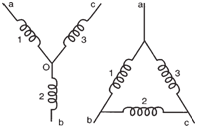Delta-connection of three coils (right), Wye-connection of three coils (left).

AC Circuits

While many forms of “alternating current” are non sinusoidal, the popular use of the term alternating current, or AC, usually
implies sinusoidal voltage or current. Electro- magnetic devices such as motors consist of ferromagnetic materials with nonlinear
voltage/current relationships. Thus, current will not be pure sinusoidal.

Root-Mean-Square or Effective Values, and Power Factor in AC Circuits:

The voltage (V) and current (I) in a sinusoidal alternating current circuit consisting of linear devices are generally written as:

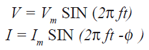Here, V_m and I_m are the peak values of V and I respectively, f is the frequency in hertz (Hz) and φ is the phase angle (in radians)
between the current and the applied voltage. (See figure below). Since the positive portion of the voltage or current is the mirror
image of the negative portion, the average value in one complete cycle is zero.

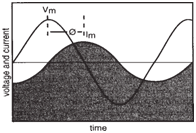V_m and I_m are out of phase by an angle φ.

This result provides no useful information about the magnitude. One useful way of specifying the magnitude of the AC is to compute its root-mean-square (rms) value which is alternatively called the effective value.

The effective value of alternating current is that which will produce the same amount of heat or power in a resistance as the corresponding value of direct current. The effective value of current (I) is obtained by first computing the average of the square of
the current and then taking the square root of the result. Without performing the computation, we will just state that the effective
value of current I_e is:

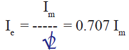Similarly, the effective voltage (V_e) is:

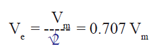Then the average power (P) of the circuit can be shown to be:

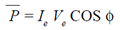The quantity (COS φ) is called the power factor of the circuit. If the current (I) and voltage (V) are in phase (i.e., f = 0) then we have the maximum power (P = I_e V_e). Stated another way, only the component of Ie in phase with Ve contributes to the average power. The other component may be said to be “watt less.”

Pure Resistance AC Circuit

A pure resistance circuit is one in which there is no significant inductive or capacitive component. In such a circuit, the current
and voltage would both be sinusoidal and in phase ( φ = 0). See figure below.

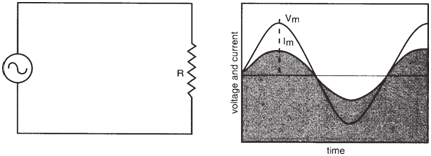Pure resistance (R) circuit. Vm and Im are in phase, φ = 0.

Pure resistance circuits can be treated as if they were DC circuits if the effective values of current and voltage (I_e and V_e) are used:

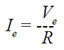Since the average power:

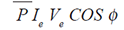then for the phase angle f = 0°:

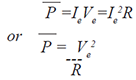Pure Inductance AC Circuit

In an inductive circuit, the counter emf (or self-inductance) of the inductor will offer opposition to any change in the current. Since an alternating current is one that is continually changing, there will be a continual opposition to the flow of current corresponding in value to the rate of change of current.

Inductive Reactance:

The opposition to the current flow in an inductance circuit is called the inductive reactance (X_L), which is given by the formula:

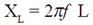where X_L is in ohms, f is the frequency in Hz and L is the inductance in Henrys.

The phase angle (φ) is +90°. Thus, a pure inductance circuit will not only offer opposition to current flow but will also cause the current to lag behind the voltage by 90° (figure below).

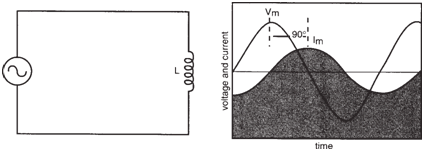Pure inductance (L) circuit. I lags V, φ = 90°.

The effective current (Ie) and average power (P) are:

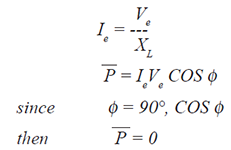Therefore, there is no power loss in a pure inductance circuit.

Pure Capacitance AC Circuit

A capacitor placed in a circuit also presents opposition to current flow. This is due to the limitation that charge will flow into the capacitor and accumulate only to the level proportional to the applied voltage. No further charge will flow in or out until there is a corresponding change in applied voltage.

Thus, the current in a capacitor circuit is proportional to the slope of the voltage curve. The slope is highest for a sinusoid when V = 0 and the current flow is at its maximum. The slope is zero when V is at its peak (positive or negative) and this corresponds to a zero current flow.

Capacitive Reactance:

The opposition to current flow in a capacitance circuit is called the cap active reactance (Xc). Its value is given by the formula:

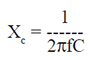where X_c is in ohms, f is the frequency in Hz and C is the capacitance in Farads.

The phase angle (f ) in this circuit is - 90°. Thus, in a pure capacitance circuit, the current leads the voltage by 90°.

The effective current (I_e ) is:

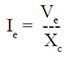Since φ = -90°, COS φ = 0. There is also no power loss in a pure capacitance circuit.

RL AC Circuit

When R and L are connected in series in an AC circuit, we have the series RL circuit shown below. Both the resistance
(R) are the inductive reactance (X_L) of the inductor offer opposition to current flow.

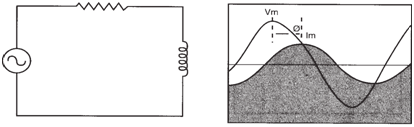Series RL circuit. I lags V. 0 < φ < 90°.

Impedance in RL Circuit:

The combined effect of R and X_L is called the impedance (Z) which is expressed in ohms:

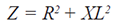The impedance can be represented as the hypotenuse of a right angle triangle whose sides are R and X_L (see figure below). This is also referred to as the impedance diagram.

The phase angle (φ) in this circuit happens to be the angle between Z and R (or, cos φ = R/Z). Since is between 0° and 90°, the current (I) in the circuit lags behind the voltage by an angle between 0° to 90° depending on the values of R and X_L.

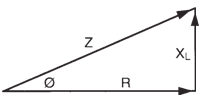Impedance diagram of an RL circuit.

The effective current (I_e) and average power (P) are:

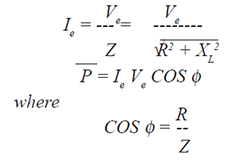Since no power is lost in the inductance, then:

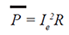RC AC Circuit

Similar to the RL circuit described previously, resistance (R) and capacitive reactance (X_c) will both oppose current flow in
an AC circuit. Unlike the RL circuit, increasing C or the frequency results in a decrease in X_c and an increase in current. See figure below.

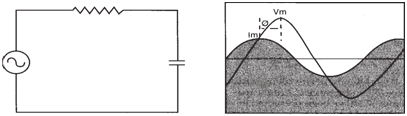RC circuit. I leads V. -90° < φ< 0.

Impedance in RC Circuit:

The impedance (Z) in this case is:

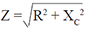The vectorial representation is shown below, where XC is pointing downwards and represents a “negative” Vector.

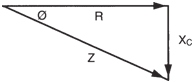Impedance diagram of an RC circuit.

The phase angle (φ) is now between - 90° and 0°, and:

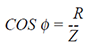The current (I) in the circuit lags the voltage by an angle (φ) between 0° and 90° depending on the values of R and XC.

The effective current (I_e) is:

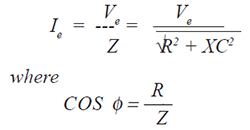Since no power is lost in the capacitance:

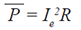RLC AC Circuit

To further generalize the AC series circuit, we should consider the RLC circuit shown below.

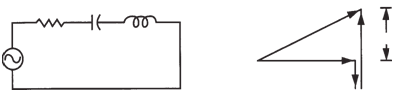Basic RLC circuit (left) and vector diagram (right).

The impedance of this circuit is:

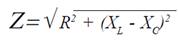The vector diagram of the above relationship is also shown in the figure above. The phase angle ( φ ) in an RLC circuit is between
-90° and +90° where:

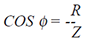If X_L > X_C, then the current in the circuit will be lagging the voltage. If X_L < X_C, then the current will be leading the voltage. If X_L = X_C, the circuit is said to be resonant and will behave as purely resistive. The effective current (I_e) is:
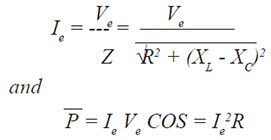