Motor Fundamentals |
| |
| BASIC
MECHANICAL
PRINCIPLES |
Until now, we have presented the electrical
characteristics of motors to acquaint
you with the fundamentals of motor action
and the effects of direct and alternating
current on motor design and operation.
Electrical characteristics affect a designer’s
decisions on which motor to choose for
any given application.
Equally important in understanding motor
operation are the mechanics and performance
characteristics of electric motors.
Mechanics encompasses the rules which
govern the motion of objects, in particular:
a). the force which must be applied to start
an object moving or to stop it, and
b). the opposing forces which must be
overcome before movement can begin
or end.
Other factors such as speed, acceleration
and amount of displacement all play a
part in determining which motor is best
suited to perform a task. |
| |
| Translational Motion |
| The movement of a uniform object
in a straight line is referred to as translational
motion. The three parameters of
translational motion are displacement, velocity
and acceleration. |
Displacement: |
| The change in
position of an object is known as displacement.
It is a vector quantity with both magnitude
and direction and is shown mathematically
as: |
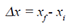 |
| where Ox is the total displacement, xf is
the object’s final position and xi is the object’s
initial position. |
Velocity: |
| The rate at which an
object’s position changes with time is its
velocity. There are two types of velocity:
average and instantaneous. Average velocity
is the net displacement divided by the
elapsed time: |
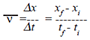 |
where d is the net displacement and t is the
elapsed time to make the displacement, tf
is the final time and ti is the initial time.
At any instant in time the velocity
of an object may exceed the average velocity,
so it is sometimes necessary to
know the instantaneous velocity: |
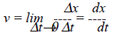 |
Speed: |
| Frequently, the terms speed
and velocity are used interchangeably. Velocity
can be positive or negative. Speed is
equal to the absolute value of the instantaneous
velocity and is always expressed as
a positive number: |
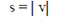 |
Acceleration: |
| As an object begins
to move, its velocity changes with respect
to time. This is called acceleration. Like
velocity, acceleration is expressed in average
and instantaneous quantities. Average
acceleration equals: |
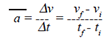 |
where Dv is the difference between the
object’s final and initial velocities, and Dt is
the elapsed time.
The instantaneous acceleration is defined
by the following formula: |
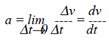 |
| |
| Rotational Motion |
| Motors can be used to move objects in
a straight line, which is why a brief overview
of translational motion was given. But
motor design and application focuses
heavily on rotational motion around an axis.
The same principles of displacement, velocity
and acceleration also govern rotational
motion. In many motion control applications,
it often becomes necessary to
transform linear motion into rotational motion
or vice versa. |
Angular Displacement: |
For
rotational motion, displacement is expressed
in radians, degrees or revolutions
because the displacement occurs in reference
to a rotational axis (one radian =
57.3°, one revolution = 360° = 2π radians.)
Angular displacement is expressed as: |
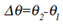 |
| where θl is the object’s initial angular
position relative to the axis and θ2 is the
final angular position. |
Angular Velocity: |
Angular velocity
is expressed in radians / second,
revolutions / second, or revolutions /
minute (RPM). It is the rate at which an
object’s angular displacement changes with respect to time. Like translational velocity,
it can be expressed as an average or instantaneous
quantity.
The formula for average angular
velocity is: |
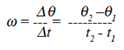 |
where Δθ is the net angular displacement
between the initial position and final position
and Δt is the elapsed time.
Instantaneous angular velocity is expressed
as follows: |
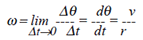 |
| where v = circumferential linear velocity. |
Angular Acceleration: |
When
an object’s angular velocity changes with
respect to time, it is undergoing angular
acceleration. Average angular acceleration
is expressed as: |
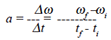 |
| An object’s instantaneous angular acceleration
an be calculated as: |
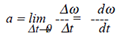 |
| |
| Statics and Dynamics |
The previous discussion focused on the
motion of an object either in a straight line
or about an axis. But other factors must be
considered when discussing motion. The
size and weight of an object determine the
amount of force needed to move it or stop
it. Other factors such as friction also play a
role in determining the amount of force
needed to move an object. We will now
center our attention on these other factors. |
Mass: |
Mass is the property of an
object that determines its resistance to motion.
It is a factor of the object’s weight
(W) and its acceleration due to gravity (g).
Mass is the quantitative measure of inertia.
It is the mass of an object that requires a
force to move it. It is usually expressed in
kilograms or pounds (mass)*.
* The pound-mass is a body of mass (0.454 kg). The pound-force is the force that gives
a standard pound-mass an acceleration equal to the standard acceleration of gravity
(32.174 ft/sec.).
In a linear system: |
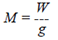 |
Momentum: |
| The fundamental
measure of an object’s motion is momentum.
In a linear system, it is the product of
the object’s mass and linear velocity and is
expressed in newton-seconds or pound seconds: |
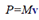 |
Force: |
| The push or pull on an object
that causes it to move or accelerate is
called force. It is directly proportional to
the object’s mass and acceleration: |
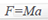 |
| where M is the object’s mass and a is the
acceleration. |
Rotational Inertia: |
| In linear motion,
the inertia of an object is represented
by the object’s mass: |
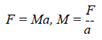 |
| It is the mass which tells us how large a
force will be required to produce constant
acceleration. The rotational analog of this
formula is: |
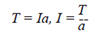 |
| This formula tells us how much torque
(T) is required to produce angular acceleration
(a). The moment of inertia (I) can be
defined as the mass of the object times the square of the distance (r) from the rotational
axis (see figure below): |
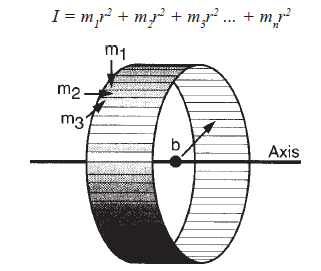 |
The moment of inertia of a
hoop containing many small masses on
its circumference. |
|
The moment of inertia can be calculated
for any object this way but calculus is usually
needed for the summation. The figure below
shows the values of I for several familiar
shapes used in mechanical systems.
The figure below shows that the moment of
inertia is always the product of the object’s
mass and the square of a length. |
|
| Moments of inertia for familiar objects. |
| For a
hoop, I = Mr2. This leads to a general
formula: |
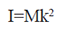 |
where k is the radius of rotation at which
the entire mass of the object should be
concentrated if the moment of inertia is to
remain unchanged. A more standard term
for this length is the radius of gyration. |
| |
| Motor Load and Torque
Characteristics |
The principles we have just discussed
can be applied specifically to motor applications.
A motor cannot be selected until
the load to be driven and the torque characteristics
are determined. |
Motor Load: |
| The term “motor load”
can refer to horsepower (hp) required by the driven object or machine. Motor load
in hp can be expressed: |
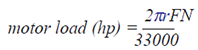 |
| where r (in feet) is the radius at which the
force (F, in pounds) is applied and N is
revolutions per minute. |
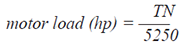 |
| Where torque (T) is expressed in lb-ft., or
if T is expressed in oz-in., then: |
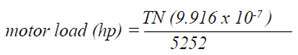 |
Motor load is best described as the
torque required by the load. The torque
requirement may be dependent upon speed
as well. Various conditions place specific
demands on torque requirements and they
are discussed next. |
Breakaway Torque: |
| This is the
torque required to start the shaft turning
and is usually the torque required to overcome
static friction. |
Accelerating Torque: |
This
torque may be expressed in percent of
running torque. It is the amount of torque
needed to accelerate the load from standstill
to full speed, and to overcome friction,
windage, product loading and inertia. |
Peak Torque: |
| Peak torque is the
maximum instantaneous torque that the
load may require. High peaks for brief periods
are acceptable, but if an application
requires sustained torque higher than a
motor’s peak rating, a different motor
should be considered. |
Constant Torque: |
| A load with a
horsepower requirement that varies linearly
with changes in speed is said to have constant
torque requirements. |
| |